一 概要介绍
我们主要关注拉普拉斯算子在图像方面的应用。首先,列出二维拉普拉斯算子的定义:
$\Delta f = \frac{\partial^2f}{\partial x^2} + \frac{\partial^2f}{\partial y^2}$
从公式中可以看到,Laplace 算子在图像上,实际就是 x, y 两个方向的二阶偏导数求和。为什么这个算子可以检测边缘呢?我们可以看一下图示:

上面左图,是图像灰度变化的曲线。在图的中心部分,灰度有一个明显的上升变化。而这个变化,我们可以认为是边缘(不严谨的说)。中心点的圆圈处,是该曲线一阶导数(梯度)最大的点。
上面右图,是对应左图的一阶导函数。我们可以看出,对应的一阶导函数的最大值,也已经用圆圈标注了。
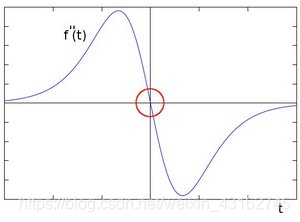
上图,是灰度曲线的二阶导函数。对应着前两幅图看,圆圈标注的依然是一阶导函数的极值点,而在该点两侧,二阶导函数的符号是相反的。
到此为止,我们可以解释为什么拉普拉斯算子可以检测边缘了。边缘处的二阶导函数是过零点,即:左右符号相反的点。注意:单单是为零的点,不足以判断边缘。因为,平滑图像一阶,二阶倒数也可能为零。
二 计算过程
由于图像可以看做是二元函数,其中 x,y 的值是离散的,最小变化量为 1。因此可以用差分代替微分的计算。求导的时候:
连续形式:
${f}’(x_{0}) = \lim_{\Delta x \to 0} \frac{f(x_{0} + \Delta x) - f(x_{0})}{\Delta x}$
离散形式:
${f}’(x_{0}) = \lim_{\Delta x \to 1} \frac{f(x_{0} + \Delta x) - f(x_{0})}{\Delta x}$
有了离散形式,我们就不难得出图的一阶偏导函数了:
$\frac{\partial f}{\partial x} = f(x+1, y) - f(x, y)$
$\frac{\partial f}{\partial y} = f(x, y+1) - f(x, y)$
然后,在一阶偏导函数的基础上,求二阶偏导函数。在求一阶偏导函数的时候,我们是通过 x+1 的形式来近似求 x 点的偏导的,直观上来讲取值有点偏右了。那么在求二阶导函数的时候,我们让 x = x - 1 来近似 x 点,更为恰当。所以,二阶偏导函数为:
$\frac{\partial^{2}f} {\partial x^{2}}=f(x+1, y) - f(x, y) - (f((x-1)+1, y) - f(x-1, y))=f(x+1, y)+f(x-1, y)-2f(x, y)$
$\frac{\partial^{2}f} {\partial y^{2}}=f(x, y+1) - f(x, y) - (f(x, (y-1)+1) - f(x, y-1))=f(x, y+1)+f(x, y-1)-2f(x, y)$
由拉普拉斯算子的定义,把上面两式求和,即:
$\Delta f = f(x+1,y) + f(x-1,y) + f(x,y+1) + f(x,y-1) - 4f(x,y)$
上面的式子,用在图像里可以看做上,下,左,右的点求和,减去四倍的中心点。因此,可以用如下模版对图像做卷积:
\[\begin{bmatrix} 0 & 1& 0\\ 1& -4& 1\\ 0& 1& 0 \end{bmatrix}\]三 运行示例
下面是一个非常简单且直白的测试图:

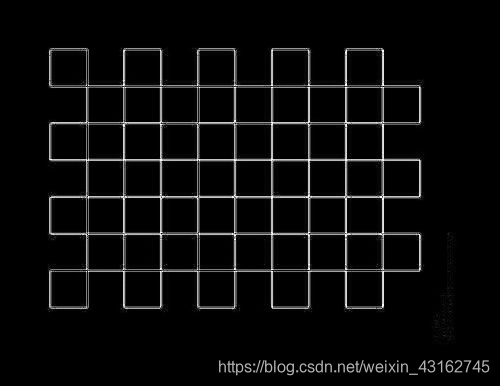
四 扩展模版
注意,扩展模版中元素和应为 0。
\[\begin{bmatrix} 0 & -1& 0\\ -1& 4& -1\\ 0& -1& 0 \end{bmatrix}\] \[\begin{bmatrix} -1 & -1& -1\\ -1& 8& -1\\ -1& -1& -1 \end{bmatrix}\]上面模版元素的符号与最初模版的符号相反。这里需要注意的是,符号相反,使得算子的结果符号也是相反的。这对于检测过零点并没有什么影响,但是如果是用该算子锐化图像,则要注意结果的加减运算。锐化是为了让灰度差异更加突出,因此,模版中心符号为负,应该减去计算结果。模版中心为正,应该加上计算结果。
\[\begin{bmatrix} 1& 1& 1\\ 1& -8& 1\\ 1& 1& 1 \end{bmatrix}\]正常的拉普拉斯算子是各向同性滤波器,意味着图像旋转并不影响结果。但默认的模版只在 90 度方向上存在这个不变性,而扩展模版则在 45 度方向上具有了该特性。
五 相关问题
1.laplace 算子为何是 x 和 y 的二阶偏导的和。
这样可以同时响应 x,y 两个方向梯度的变化。通常来讲,边缘的特性是在同一点,只有一个边缘梯度方向。比如说是水平的,或者垂直的,或者 45 度这样的,这些情况都没有问题。但有一个极特殊情况,那就是 x,y 方向的二阶偏导是相互抵消的,导致边缘没有响应,或者响应变弱了。这种情况虽然极少,但确实是存在的。好在即使存在,也只可能是个别点,基本可以忽略。
2.laplace 算子的优劣之处
由于 laplace 使用二阶偏导找过零点,那么对一些很小的灰度变化,也能灵敏的响应。但这也导致了其对噪声很敏感,尤其是孤立的噪声点特别强烈。因此,最好提前进行平滑处理,比如使用高斯滤波。高斯和拉普拉斯算子结合在一起,就是 LoG 算子,这个后面再说。
由于 laplace 使用二阶偏导数,使其对应平缓的梯度变化不敏感,这是区别于一阶导数的地方。因此,如果不想检测出平缓的粗边缘,使用二阶导数更合适。
laplace 可以通过两侧的符号判断边缘灰度是增还是减,有一定的实际用途。
六 参考资料:
转载请注明来源: https://xudeyu.github.io/2019/03/31/laplace-operator.html 欢迎对文章中的引用来源进行考证,欢迎指出任何有错误或不够清晰的表达。可以在下面评论区评论(可能需要在能访问 disqus 服务的网络),也可以邮件至 。

